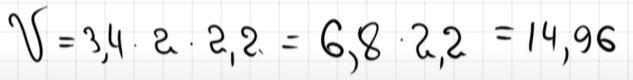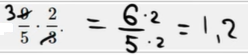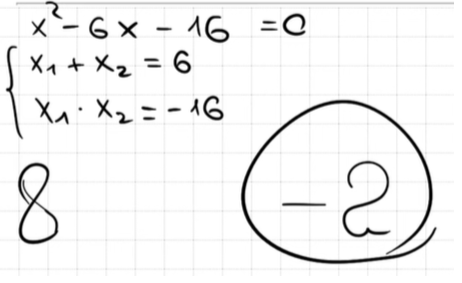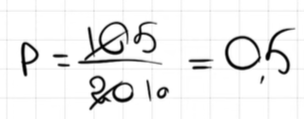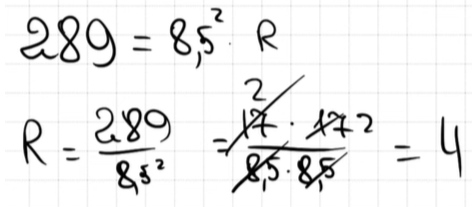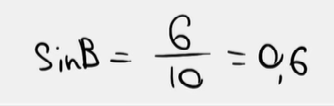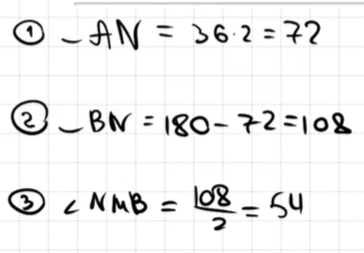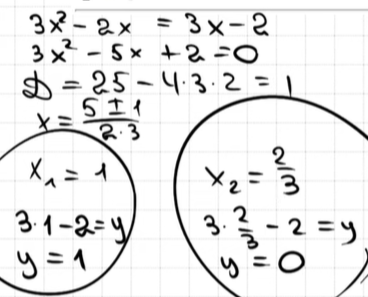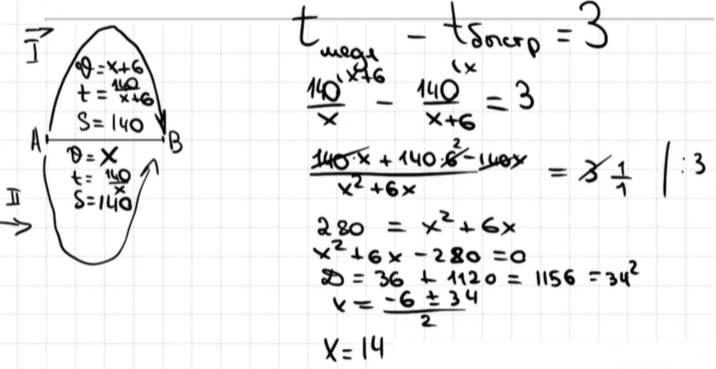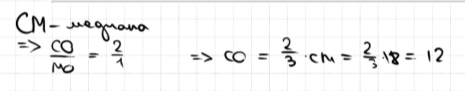ПРОБНЫЙ ВАРИАНТ ОГЭ (2024) по математике с ответами

Вашему вниманию представлен пробный вариант ОГЭ (2024) по математике с ответами.

Инструкция по выполнению работы

Вариант 1

Часть 1

Хозяин дачного участка строит баню с парным отделением. Размеры парного отделения: длина 3,4 м, ширина 2 м, высота 2,2 м. Для разогрева парного помещения можно использовать электрическую или дровяную печь. Три возможных варианта даны в таблице.

Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведение специального кабеля, что обойдётся в 6000 руб. Кроме того, хозяин подсчитал, что за год электрическая печь израсходует 2800 киловатт-часов электроэнергии по 3 руб. за 1 киловатт-час, а дровяная печь за год израсходует 3,5 куб. м дров, которые обойдутся по 1600 руб. за 1 куб. м.

1. Найдите объём парного отделения строящейся бани (в куб. м).

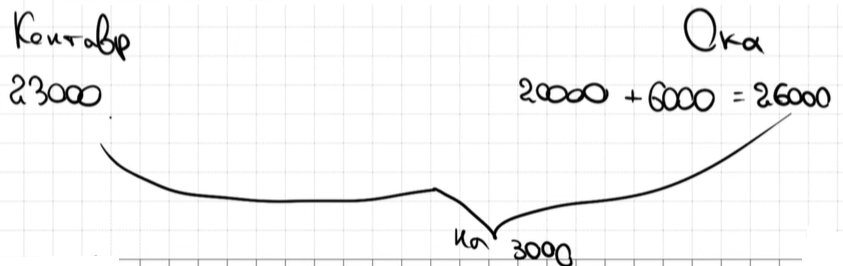
2. На сколько рублей дровяная печь, подходящая по отапливаемому объёму парного отделения, обойдётся дешевле электрической с учётом установки?

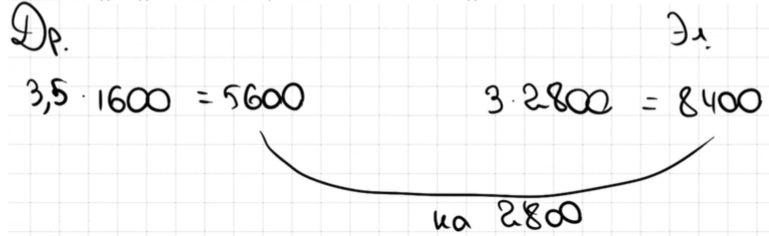
3. На сколько рублей эксплуатация дровяной печи, которая подходит по отапливаемому объёму парного отделения, обойдётся дешевле эксплуатации электрической в течение года?

4. Доставка печи из магазина до участка стоит 900 рублей. При покупке печи ценой выше 20000 рублей магазин предлагает скидку 3% на товар и 25% на доставку. Сколько будет стоить покупка печи «Кентавр» вместе с доставкой на этих условиях?

5. Хозяин выбрал дровяную печь. Чертёж печи показан на рис. 2. Размеры указаны в см.

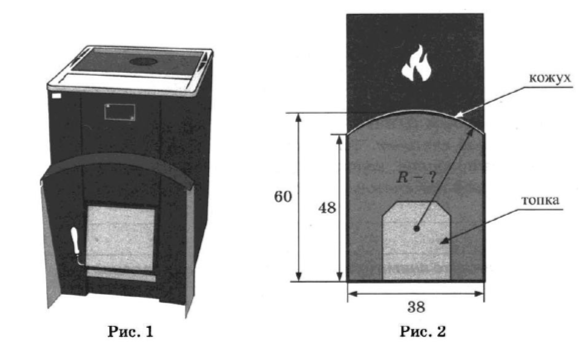
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке по дуге окружности (см. рис.). Для установки печки хозяину понадобилось узнать радиус закругления арки 𝑅. Размеры кожуха показаны на рисунке. Найдите радиус в сантиметрах; ответ округлите до десятых.

6. Найдите значение выражения

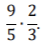
7.

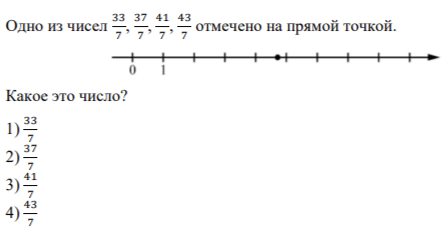
8. Найдите значение выражения

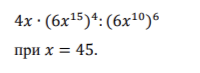
9. Решите уравнение

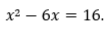
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

10. Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием учебного года, из них 10 с машинами и 10 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Коля. Найдите вероятность того, что Коле достанется пазл с машиной.

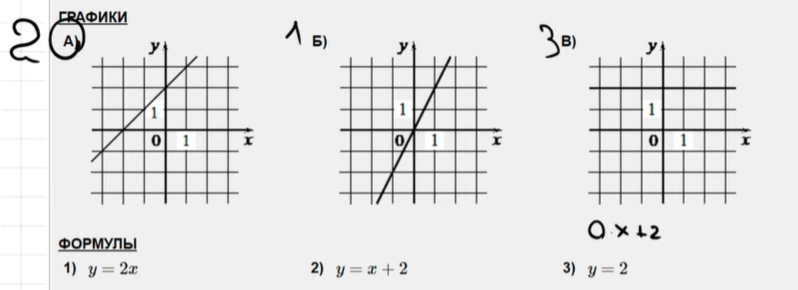
11. Установите соответствие между графиками функций и формулами, которые их задают.

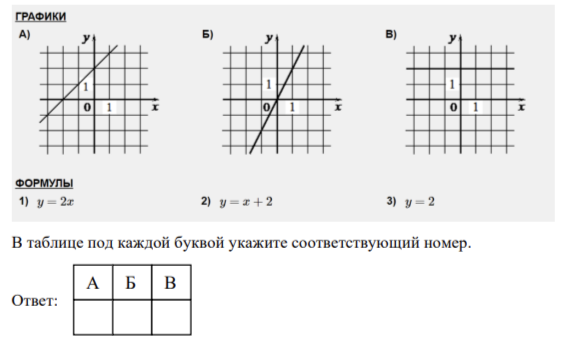
12.

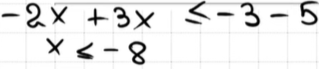
13. Укажите решение неравенства

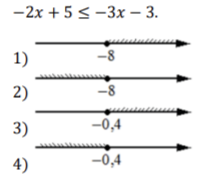
14. В 7:00 часы сломались и за каждый следующий час отставали на одно и тоже количество минут по сравнению с предыдущим часом. В 22:00 того же дня часы отставали на час. На сколько минут отставали часы спустя 17 часов после того, как они сломались?

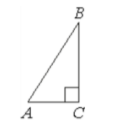
15. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐴𝐶 = 6, 𝐴𝐵 = 10. Найдите sin 𝐵

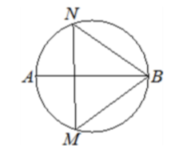
16. На окружности по разные стороны от диаметра 𝐴𝐵 взяты точки 𝑀 и 𝑁. Известно, что ∠𝑁𝐵𝐴 = 36°. Найдите угол 𝑁𝑀𝐵. Ответ дайте в градусах.

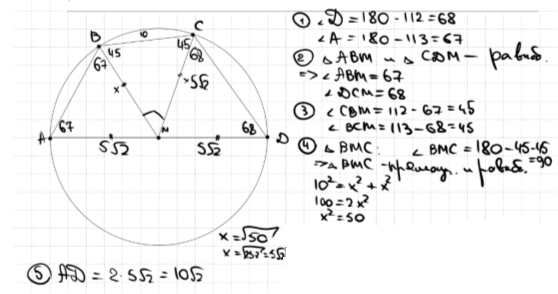
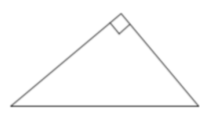
17. Два катета прямоугольного треугольника равны 6 и 7. Найдите площадь этого треугольника.

18. На клетчатой бумаге с размером клетки 1 × 1 изображена фигура. Найдите её площадь.

19. Какое из следующих утверждений верно?

1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) В любой прямоугольник можно вписать окружность.
3) Каждая из биссектрис равнобедренного треугольника является его медианой.

В ответ запишите номер выбранного утверждения.

Часть 2

20. Решите систему уравнений

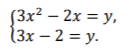
21. Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью на 6 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

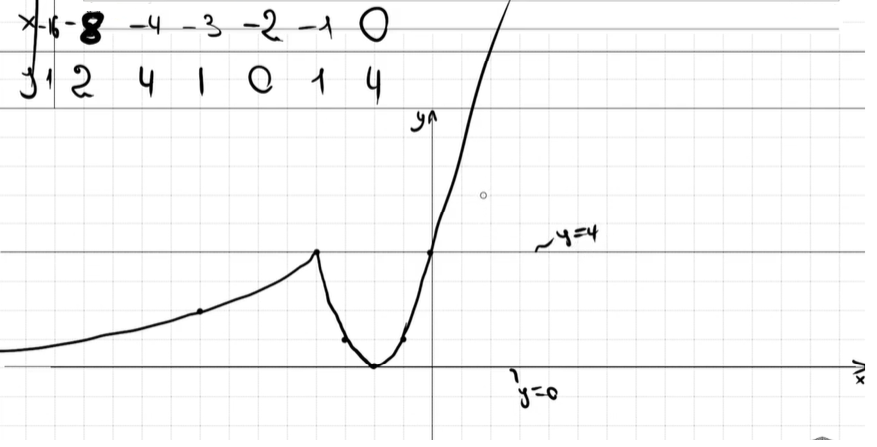
22. Постройте график функции. Определите, при каких значениях 𝑚 прямая 𝑦 = 𝑚 имеет с графиком одну или две общие точки.

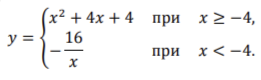
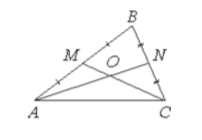
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.

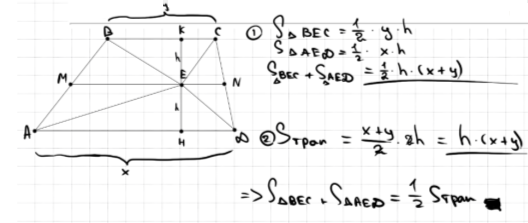
24. На средней линии трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 выбрали произвольную точку 𝐸. Докажите, что сумма площадей треугольников 𝐵𝐸𝐶 и 𝐴𝐸𝐷 равна половине площади трапеции.

25. Середина 𝑀 стороны 𝐴𝐷 выпуклого четырёхугольника 𝐴𝐵𝐶𝐷 равноудалена от всех его вершин. Найдите 𝐴𝐷, если 𝐵𝐶 = 10, а углы 𝐵 и 𝐶 четырёхугольника равны соответственно 112° и 113°.